I have been a university math professor for over twenty-five years, and I love it. I get to work with students from across the spectrum of mathematical comfort. I teach students who love math and take lots of advanced classes, and I teach students who have not had good experiences at all and, quite honestly, fear the subject. Each student is different, of course, and I am so glad for opportunities to work with them all.
As different as student experiences can be, there is one thing that unites them all – Monday mornings are hard! In Monday morning classes, there is a palpable sense of exhaustion (dread, even) regarding the upcoming week of assignments and exams. There is a common sense of regret that the prior weekend was not as productive as had been originally planned (we teachers feel this too!). This makes Monday classes particularly challenging.
Several years ago, I decided to start a Monday morning class with a magic trick – one that was math related. This perked up the group a bit, and a student suggested that I should do something similar every Monday. With that, “Magic Mondays” were born.
Since that day, I have started every Monday morning class (from introductory to advanced) with a magic effect that is related in some way to math. Sometimes the math part is clear (effects of the form “Pick a number, now multiply it by 5, now add 3, etc.”). Other times, though, the mathematical part is in the working and is less obvious.
What started as a way to ease students into Monday mornings has become a staple of my teaching career. Students who are taking their first class with me will ask me about it when the semester starts. Clearly, they have heard about Magic Mondays from others, and that lets me know that the lessons (or at least the experiences) are making it out the classroom door.
I have discovered over the years that the impact of magic in a math classroom is more than just a fun extracurricular diversion. This magic is also making better math students, and this article describes a few ways in which this is the case.
I want to be clear that when I say “better” math students, I’m not just talking about students getting better grades. Good grades are nice, of course, but I’m referring to improvements that, to me, are much more meaningful. I have organized my comments based on six Cs: comfort, coolness, concepts, curiosity, creativity, and communication.
Comfort
If I had a nickel for every time someone said to me, “I’m not a math person” – then I could fill hundreds of miser’s dream buckets with coins. I have come to understand that the statement really means “math makes me uncomfortable.” This is often the result of negative experiences in classes (or with teachers), and unfortunately, it is all too common.
One of my goals as a teacher is to help change this perspective, for this surely makes better math students. I want the magic (and the mathematics) that I do in class to be inviting, welcoming – and comfortable – for the students. I do my best to avoid “gotcha”-type effects, especially in introductory classes of hesitant students. If I can make students comfortable by enjoying some magic, then I am one step closer to having them feel more comfortable with the math behind it. Comfortable math students are better math students.
Coolness
When a student tells me that math is not their thing, I like to add the word “yet” to their statement. I suggest that perhaps they have not yet encountered a part of mathematics that has caught their attention, and then I like to try and find something that will do just that. If I can help students find something “cool” about math, then they are less likely to have the “not a math person” perspective – and that makes them better math students.
⦁ Take any number that is not evenly divisible by 7, get a calculator, and then divide that number by 7. If the calculator window is large enough, you’ll see lots of numbers to the right of the decimal (they actually go on forever, but no calculator window is that large!). Find the sum of the first six digits to the right of the decimal. You’ll always get 27. Cool math area: cyclic numbers.
⦁ Start with a three-digit number, perform a particular set of easy operations, and always end up with the number 1089. (The operations are readily available via an internet search of the number 1089.) Cool math area: basic algebra is used to show why this works.
⦁ Fold a piece of paper a certain way, and make a single, straight scissor cut. Unfold the paper to reveal a swan, a butterfly, a star, or many other things. Cool math area: the Fold and Cut Theorem.
⦁ Start with a standard deck of 52 playing cards and do eight successive faro shuffles to really mix them up (wink-wink). The cards are now in their original positions! Cool math area: several great (advanced) mathematical topics related to card shuffling. Coolness is in the eye of the beholder, of course, and so I try to use an assortment of different ideas to help students see a new side of math.
Concepts
Magic Mondays can work nicely as introductions to class topics. When students have relatable examples in mind, new concepts are less abstract for them from the beginning.
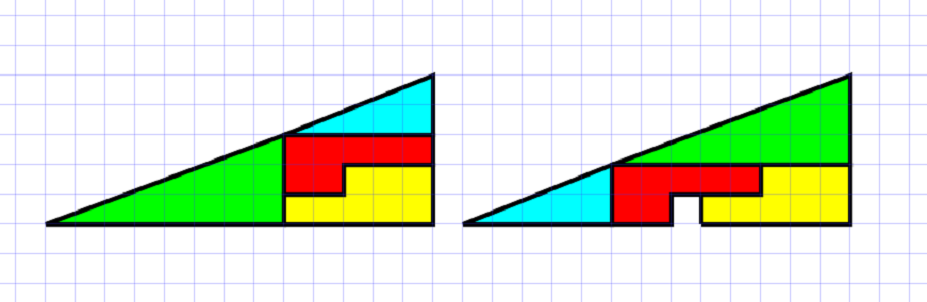
⦁ Angles, Area, Slope: The pieces in the puzzle on the left can be rearranged into the positions on the right – and there is something missing! These “geometric vanishes” have appeared in various forms over the years, but the reason for their weirdness is all based on angles, areas, and slopes of lines. This effect is a nice introduction to some of these topics.
⦁ Modular Arithmetic: I tell my class that I have a very strange hobby – I memorize Universal Product Codes (UPCs) that appear on retail items. They can test me by calling out the codes on items in their possession and omitting one of the digits (and instead saying “blank” at that position). After a series of questions meant only for show (and a little bit of basic mental calculation), I can announce the missing digit. I’m not sure I fool anyone with my “strange hobby” claim, but this is a fun introduction to the area of modular arithmetic, which is the thing upon which the patterns of UPCs are based.
(The code below is for Bicycle playing cards. Do some research on these patterns and see if you can find the missing digit!)

Curiosity
A curious mind is one of the best things a math student can possess. Genuine curiosity involves not only a desire to know more about something but also a willingness to persevere on the journey toward that knowledge. Sometimes (many times?) in math classes, impatience wins out over curiosity. Understandably, it may be difficult for a student to generate genuine curiosity about a word problem involving two trains approaching one another on parallel tracks. Nurturing curiosity takes practice, though. If I can encourage curiosity in other settings, maybe that skill and the associated perseverance can be more fully developed.
An example I have used in class in this setting is an effect like David Copperfield’s Orient Express trick (not the one where an actual train disappears, but the one involving a grid of cards similar to the one below. A card is randomly chosen, and, after several steps/moves, Copperfield identifies the current location).

This is nice because it can be repeated at students’ desks with their own cards, and the effect/method is in the sweet spot between being too easy and too complex. I have found that this puts their curiosity level at just the right place, and they enjoy working toward understanding the reasoning (which, by the way, is based on the relationship between even and odd numbers).
Creativity
It is surprising for many students to hear that creativity is fundamental in mathematics. Often thought of as a subject “where there is always only one right answer,” there is a common perception that math is a straight-down-the-middle, solve-it-or-you-don’t endeavor. With the possible exception of a claimed ability to bend spoons with your mind, nothing could be further from the truth. Mathematicians are problem solvers, and while some problems have standard solution methods, others require a great deal of creativity and outside-of-the-box thinking. (Here you can picture the scene in the classic film Apollo 13 where the mathematicians and engineers are challenged to create a survival plan using only items that were in the stranded capsule.) In my classes, I love to try and find opportunities for students to practice this sort of creativity. Not only does it help them in my class, but it also helps them to become better thinkers and problem solvers in general.
I often use Magic Monday opportunities to do this. After I demonstrate an effect, I give students time to brainstorm a bit to come up with as many ways as they can as to how the trick worked. The goal is not for them to find the way I did it, but rather to identify ways that I might have done it. A great example of this is Fitch Cheney’s Five Card Trick. This is the effect in which the magician, after seeing four of five randomly selected cards, can identify the fifth. The effect requires an assistant who is in-the-know, and it uses a mathematical system to use four cards to encode the identity of the fifth. I enjoy hearing the possible methods that the students suggest, and it gets their creative juices flowing.
Another way to tap into students’ creativity is to ask them to modify my effects to create new ones. For the five-card trick, I ask them if they could do the same trick with fewer (or more) cards. They like the idea of encoding the identity of things using other things, and they think of lots of different ways to use these codes.
Communication
As students progress through math courses and math majors, they begin to understand the importance of precise communication. In mathematical writing, symbols and terms have precise meanings, and any sort of sloppiness in their use can turn a true statement into a false (or nonsensical) one. I use Magic Mondays to give students a chance to practice this precision, and I do this by having them write clear, detailed instructions regarding how an effect looks in performance and how the trick is accomplished.
One example that I use a lot in this setting is the classic 21 card trick. The effect is simple to do, but it can be a challenging exercise to write the instructions for someone who has never seen or heard of it. As students prepare drafts, we have other students try to read and follow the instructions as literally as possible. Errors and lack of precision get revealed very quickly this way, and this is both instructive and fun.
Magic, math, and teaching are three of my favorite things. I feel very fortunate to be able to combine all of these things with my Magic Mondays. From hesitant to eager students and from introductory to advanced levels, magic can enrich perceptions, foster creativity, and deepen understanding of the beautiful subject of mathematics.
Recent Comments